Appendix A — Numpy - multidimensional data arrays for python
|
|

|
A.1 Introduction
Python objects:
- High-level objects: integers, floating-point
- Containers: lists (costless append), dictionaries (fast lookup)
- Python lists are very general. They can contain any kind of object and are dynamically typed
- However, they do not support mathematical functions such as matrix and dot multiplications. Implementing such functions for Python lists would not be very efficient because of the dynamic typing
NumPy provides:
- Extension package to Python for multi-dimensional arrays
- Numpy arrays are statically typed and homogeneous. The type of the elements is determined when the array is created
- Because of the static typing, fast implementation of mathematical functions such as multiplication and addition of
numpyarrays can be implemented in a compiled language (C and Fortran is used). Moreover, Numpy arrays are memory efficient
The numpy package (module) is used in almost all numerical computation using Python. It is a package that provides high-performance vector, matrix and higher-dimensional data structures for Python. It is implemented in C and Fortran so when calculations are vectorized (formulated with vectors and matrices) which provides good performance
To use numpy you need to import the module, using for example:
426 µs ± 19.1 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)255 µs ± 14.9 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)In the numpy package the terminology used for vectors, matrices and higher-dimensional data sets is array.
A.2 Documentation
Docstring:
array(object, dtype=None, copy=True, order='K', subok=False, ndmin=0)
Create an array.
Parameters
----------
object : array_like
An array, any object exposing the array interface, an object whose
__array__ method returns an array, or any (nested) sequence.
dtype : data-type, optional
The desired data-type for the array. If not given, then the type will
be determined as the minimum type required to hold the objects in the
sequence.
copy : bool, optional
If true (default), then the object is copied. Otherwise, a copy will
only be made if __array__ returns a copy, if obj is a nested sequence,
or if a copy is needed to satisfy any of the other requirements
(`dtype`, `order`, etc.).
order : {'K', 'A', 'C', 'F'}, optional
Specify the memory layout of the array. If object is not an array, the
newly created array will be in C order (row major) unless 'F' is
specified, in which case it will be in Fortran order (column major).
If object is an array the following holds.
===== ========= ===================================================
order no copy copy=True
===== ========= ===================================================
'K' unchanged F & C order preserved, otherwise most similar order
'A' unchanged F order if input is F and not C, otherwise C order
'C' C order C order
'F' F order F order
===== ========= ===================================================
When ``copy=False`` and a copy is made for other reasons, the result is
the same as if ``copy=True``, with some exceptions for `A`, see the
Notes section. The default order is 'K'.
subok : bool, optional
If True, then sub-classes will be passed-through, otherwise
the returned array will be forced to be a base-class array (default).
ndmin : int, optional
Specifies the minimum number of dimensions that the resulting
array should have. Ones will be pre-pended to the shape as
needed to meet this requirement.
Returns
-------
out : ndarray
An array object satisfying the specified requirements.
See Also
--------
empty_like : Return an empty array with shape and type of input.
ones_like : Return an array of ones with shape and type of input.
zeros_like : Return an array of zeros with shape and type of input.
full_like : Return a new array with shape of input filled with value.
empty : Return a new uninitialized array.
ones : Return a new array setting values to one.
zeros : Return a new array setting values to zero.
full : Return a new array of given shape filled with value.
Notes
-----
When order is 'A' and `object` is an array in neither 'C' nor 'F' order,
and a copy is forced by a change in dtype, then the order of the result is
not necessarily 'C' as expected. This is likely a bug.
Examples
--------
>>> np.array([1, 2, 3])
array([1, 2, 3])
Upcasting:
>>> np.array([1, 2, 3.0])
array([ 1., 2., 3.])
More than one dimension:
>>> np.array([[1, 2], [3, 4]])
array([[1, 2],
[3, 4]])
Minimum dimensions 2:
>>> np.array([1, 2, 3], ndmin=2)
array([[1, 2, 3]])
Type provided:
>>> np.array([1, 2, 3], dtype=complex)
array([ 1.+0.j, 2.+0.j, 3.+0.j])
Data-type consisting of more than one element:
>>> x = np.array([(1,2),(3,4)],dtype=[('a','<i4'),('b','<i4')])
>>> x['a']
array([1, 3])
Creating an array from sub-classes:
>>> np.array(np.mat('1 2; 3 4'))
array([[1, 2],
[3, 4]])
>>> np.array(np.mat('1 2; 3 4'), subok=True)
matrix([[1, 2],
[3, 4]])
Type: builtin_function_or_methodA.3 Creating numpy arrays
There are a number of ways to initialize new numpy arrays, for example, from
- A Python list or tuples
- Using functions that are dedicated to generating
numpyarrays, such asarange,linspace, etc. - Reading data from files (
npy)
A.3.1 From Python list
For example, to create new vector and matrix arrays from Python lists, we can use the numpy.array function.
# a vector: the argument to the array function is a Python list
v = np.array([1,2,3,4])
v, type(v), v.dtype, v.shape(array([1, 2, 3, 4]), numpy.ndarray, dtype('int32'), (4,))# a matrix: the argument to the array function is a nested Python list
M = np.array([[1, 2], [3, 4]])
M, type(M), M.dtype, M.shape(array([[1, 2],
[3, 4]]),
numpy.ndarray,
dtype('int32'),
(2, 2))Note that the v and M objects are both of the type ndarray that the numpy module provides. The difference between the v and M arrays is only their shapes. We can get information about the shape of an array by using the ndarray.shape property.
Since it is statically typing, we can explicitly define the type of the array data when we create it, using the dtype keyword argument:
Common data types that can be used with dtype are: int, float, complex, bool, etc.
We can also explicitly define the bit size of the data types, for example: int64, int16, float128, complex128.
A.3.2 Using array-generating functions
For larger arrays, it is impractical to initialize the data manually using explicit python lists. Instead, we can use one of the many functions in numpy that generate arrays of different forms. Some of the more common are:
array([-1.00000000e+00, -9.00000000e-01, -8.00000000e-01, -7.00000000e-01,
-6.00000000e-01, -5.00000000e-01, -4.00000000e-01, -3.00000000e-01,
-2.00000000e-01, -1.00000000e-01, -2.22044605e-16, 1.00000000e-01,
2.00000000e-01, 3.00000000e-01, 4.00000000e-01, 5.00000000e-01,
6.00000000e-01, 7.00000000e-01, 8.00000000e-01, 9.00000000e-01])# using linspace, both end points ARE included
np.linspace(0, 10, 25) # arguments: start, end, number of samplesarray([ 0. , 0.41666667, 0.83333333, 1.25 , 1.66666667,
2.08333333, 2.5 , 2.91666667, 3.33333333, 3.75 ,
4.16666667, 4.58333333, 5. , 5.41666667, 5.83333333,
6.25 , 6.66666667, 7.08333333, 7.5 , 7.91666667,
8.33333333, 8.75 , 9.16666667, 9.58333333, 10. ])array([[0.95856122, 0.46008766, 0.18125959, 0.29118265, 0.12936857],
[0.66136799, 0.31069994, 0.02396709, 0.19487356, 0.2781103 ],
[0.95491478, 0.39030392, 0.98749426, 0.11391192, 0.71392245],
[0.45548694, 0.26654714, 0.39209578, 0.09068336, 0.1440259 ],
[0.65795932, 0.07484714, 0.33585994, 0.38683142, 0.25092455]])array([[-0.1083494 , -1.4625737 , -1.52901998, -0.19867851, -0.69311333],
[ 0.22918277, -0.54191491, -0.11518915, -0.39199225, -0.46892591],
[-1.74171355, 0.04522399, -1.30233269, -0.56877774, -0.96248809],
[ 0.47210184, -0.67675756, 0.25428361, 0.42873618, 0.94328066],
[ 1.04585954, -1.53339424, 1.22914079, 0.83127729, -0.45995271]])A.3.2.1 diag
A.3.2.2 zeros and ones
array([0.49969432, 0.25593713, 0.25810063, 0.09692171, 0.56418511])A.4 Manipulating arrays
A.4.1 Indexing and slicing
- Note that the indices begin at 0, like other Python sequences (and C/C++). In contrast, in Fortran or Matlab, indices start at 1.
- In 2D, the first dimension corresponds to rows, the second to columns.
We can index elements in an array using square brackets and indices:
# v is a vector, and has only one dimension, taking one index
v = np.random.rand(5) #Note it starts with zero
v, v[3](array([0.91365081, 0.35071951, 0.11460437, 0.71260839, 0.10188615]),
0.7126083905021839)(array([[0.40570044, 0.66548144, 0.13835937, 0.83043309, 0.12319969],
[0.58779155, 0.06309849, 0.49710274, 0.92839462, 0.80603084],
[0.19839124, 0.34528354, 0.53473647, 0.97858347, 0.5030445 ],
[0.3474475 , 0.21278653, 0.17745402, 0.1040286 , 0.18745545],
[0.04031375, 0.23991727, 0.5462427 , 0.20778317, 0.99270398]]),
0.9785834687356999)We can get rows and columns as follows
Index slicing is the technical name for the syntax M[lower:upper:step] to extract part of an array:
We can omit any of the three parameters in M[lower:upper:step]:
Negative indices counts from the end of the array (positive index from the begining):
Index slicing works exactly the same way for multidimensional arrays:
array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24],
[30, 31, 32, 33, 34],
[40, 41, 42, 43, 44]])- Chcek “Fancy indexing” at https://scipy-lectures.org/intro/numpy/array_object.html#fancy-indexing
A.5 Linear algebra on array
Vectorizing code is the key to writing efficient numerical calculations with Python/Numpy. That means that as much as possible of a program should be formulated in terms of matrix and vector operations, like matrix-matrix multiplication.
A.5.1 Scalar and array operations
We can use the usual arithmetic operators to multiply, add, subtract, and divide arrays with scalar numbers.
[[ 0 2 4 6 8]
[20 22 24 26 28]
[40 42 44 46 48]
[60 62 64 66 68]
[80 82 84 86 88]]
[[ 2 3 4 5 6]
[12 13 14 15 16]
[22 23 24 25 26]
[32 33 34 35 36]
[42 43 44 45 46]]A.5.1.1 Element-wise array-array operations
When we add, subtract, multiply and divide arrays with each other, the default behavior is element-wise operations:
array([[ 0, 1, 4, 9, 16],
[ 100, 121, 144, 169, 196],
[ 400, 441, 484, 529, 576],
[ 900, 961, 1024, 1089, 1156],
[1600, 1681, 1764, 1849, 1936]])If we multiply arrays with compatible shapes, we get an element-wise multiplication of each row:
(array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24],
[30, 31, 32, 33, 34],
[40, 41, 42, 43, 44]]),
array([0, 1, 2, 3, 4]))array([[ 0, 1, 4, 9, 16],
[ 0, 11, 24, 39, 56],
[ 0, 21, 44, 69, 96],
[ 0, 31, 64, 99, 136],
[ 0, 41, 84, 129, 176]])A.5.2 Matrix algebra
What about matrix multiplication? There are two ways. We can either use the dot function, which applies a matrix-matrix, matrix-vector, or inner vector multiplication to its two arguments:
array([[ 300, 310, 320, 330, 340],
[1300, 1360, 1420, 1480, 1540],
[2300, 2410, 2520, 2630, 2740],
[3300, 3460, 3620, 3780, 3940],
[4300, 4510, 4720, 4930, 5140]])array([[ 0, 10, 20, 30, 40],
[ 1, 11, 21, 31, 41],
[ 2, 12, 22, 32, 42],
[ 3, 13, 23, 33, 43],
[ 4, 14, 24, 34, 44]])Alternatively, we can cast the array objects to the type matrix. This changes the behavior of the standard arithmetic operators +, -, * to use matrix algebra. (Become matrix operation!)
Help on class matrix in module numpy:
class matrix(ndarray)
| matrix(data, dtype=None, copy=True)
|
| matrix(data, dtype=None, copy=True)
|
| .. note:: It is no longer recommended to use this class, even for linear
| algebra. Instead use regular arrays. The class may be removed
| in the future.
|
| Returns a matrix from an array-like object, or from a string of data.
| A matrix is a specialized 2-D array that retains its 2-D nature
| through operations. It has certain special operators, such as ``*``
| (matrix multiplication) and ``**`` (matrix power).
|
| Parameters
| ----------
| data : array_like or string
| If `data` is a string, it is interpreted as a matrix with commas
| or spaces separating columns, and semicolons separating rows.
| dtype : data-type
| Data-type of the output matrix.
| copy : bool
| If `data` is already an `ndarray`, then this flag determines
| whether the data is copied (the default), or whether a view is
| constructed.
|
| See Also
| --------
| array
|
| Examples
| --------
| >>> a = np.matrix('1 2; 3 4')
| >>> a
| matrix([[1, 2],
| [3, 4]])
|
| >>> np.matrix([[1, 2], [3, 4]])
| matrix([[1, 2],
| [3, 4]])
|
| Method resolution order:
| matrix
| ndarray
| builtins.object
|
| Methods defined here:
|
| __array_finalize__(self, obj)
| None.
|
| __getitem__(self, index)
| Return self[key].
|
| __imul__(self, other)
| Return self*=value.
|
| __ipow__(self, other)
| Return self**=value.
|
| __mul__(self, other)
| Return self*value.
|
| __pow__(self, other)
| Return pow(self, value, mod).
|
| __rmul__(self, other)
| Return value*self.
|
| __rpow__(self, other)
| Return pow(value, self, mod).
|
| all(self, axis=None, out=None)
| Test whether all matrix elements along a given axis evaluate to True.
|
| Parameters
| ----------
| See `numpy.all` for complete descriptions
|
| See Also
| --------
| numpy.all
|
| Notes
| -----
| This is the same as `ndarray.all`, but it returns a `matrix` object.
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> y = x[0]; y
| matrix([[0, 1, 2, 3]])
| >>> (x == y)
| matrix([[ True, True, True, True],
| [False, False, False, False],
| [False, False, False, False]])
| >>> (x == y).all()
| False
| >>> (x == y).all(0)
| matrix([[False, False, False, False]])
| >>> (x == y).all(1)
| matrix([[ True],
| [False],
| [False]])
|
| any(self, axis=None, out=None)
| Test whether any array element along a given axis evaluates to True.
|
| Refer to `numpy.any` for full documentation.
|
| Parameters
| ----------
| axis : int, optional
| Axis along which logical OR is performed
| out : ndarray, optional
| Output to existing array instead of creating new one, must have
| same shape as expected output
|
| Returns
| -------
| any : bool, ndarray
| Returns a single bool if `axis` is ``None``; otherwise,
| returns `ndarray`
|
| argmax(self, axis=None, out=None)
| Indexes of the maximum values along an axis.
|
| Return the indexes of the first occurrences of the maximum values
| along the specified axis. If axis is None, the index is for the
| flattened matrix.
|
| Parameters
| ----------
| See `numpy.argmax` for complete descriptions
|
| See Also
| --------
| numpy.argmax
|
| Notes
| -----
| This is the same as `ndarray.argmax`, but returns a `matrix` object
| where `ndarray.argmax` would return an `ndarray`.
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.argmax()
| 11
| >>> x.argmax(0)
| matrix([[2, 2, 2, 2]])
| >>> x.argmax(1)
| matrix([[3],
| [3],
| [3]])
|
| argmin(self, axis=None, out=None)
| Indexes of the minimum values along an axis.
|
| Return the indexes of the first occurrences of the minimum values
| along the specified axis. If axis is None, the index is for the
| flattened matrix.
|
| Parameters
| ----------
| See `numpy.argmin` for complete descriptions.
|
| See Also
| --------
| numpy.argmin
|
| Notes
| -----
| This is the same as `ndarray.argmin`, but returns a `matrix` object
| where `ndarray.argmin` would return an `ndarray`.
|
| Examples
| --------
| >>> x = -np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, -1, -2, -3],
| [ -4, -5, -6, -7],
| [ -8, -9, -10, -11]])
| >>> x.argmin()
| 11
| >>> x.argmin(0)
| matrix([[2, 2, 2, 2]])
| >>> x.argmin(1)
| matrix([[3],
| [3],
| [3]])
|
| flatten(self, order='C')
| Return a flattened copy of the matrix.
|
| All `N` elements of the matrix are placed into a single row.
|
| Parameters
| ----------
| order : {'C', 'F', 'A', 'K'}, optional
| 'C' means to flatten in row-major (C-style) order. 'F' means to
| flatten in column-major (Fortran-style) order. 'A' means to
| flatten in column-major order if `m` is Fortran *contiguous* in
| memory, row-major order otherwise. 'K' means to flatten `m` in
| the order the elements occur in memory. The default is 'C'.
|
| Returns
| -------
| y : matrix
| A copy of the matrix, flattened to a `(1, N)` matrix where `N`
| is the number of elements in the original matrix.
|
| See Also
| --------
| ravel : Return a flattened array.
| flat : A 1-D flat iterator over the matrix.
|
| Examples
| --------
| >>> m = np.matrix([[1,2], [3,4]])
| >>> m.flatten()
| matrix([[1, 2, 3, 4]])
| >>> m.flatten('F')
| matrix([[1, 3, 2, 4]])
|
| getA = A(self)
| Return `self` as an `ndarray` object.
|
| Equivalent to ``np.asarray(self)``.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : ndarray
| `self` as an `ndarray`
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.getA()
| array([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
|
| getA1 = A1(self)
| Return `self` as a flattened `ndarray`.
|
| Equivalent to ``np.asarray(x).ravel()``
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : ndarray
| `self`, 1-D, as an `ndarray`
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.getA1()
| array([ 0, 1, 2, ..., 9, 10, 11])
|
| getH = H(self)
| Returns the (complex) conjugate transpose of `self`.
|
| Equivalent to ``np.transpose(self)`` if `self` is real-valued.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : matrix object
| complex conjugate transpose of `self`
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4)))
| >>> z = x - 1j*x; z
| matrix([[ 0. +0.j, 1. -1.j, 2. -2.j, 3. -3.j],
| [ 4. -4.j, 5. -5.j, 6. -6.j, 7. -7.j],
| [ 8. -8.j, 9. -9.j, 10.-10.j, 11.-11.j]])
| >>> z.getH()
| matrix([[ 0. -0.j, 4. +4.j, 8. +8.j],
| [ 1. +1.j, 5. +5.j, 9. +9.j],
| [ 2. +2.j, 6. +6.j, 10.+10.j],
| [ 3. +3.j, 7. +7.j, 11.+11.j]])
|
| getI = I(self)
| Returns the (multiplicative) inverse of invertible `self`.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : matrix object
| If `self` is non-singular, `ret` is such that ``ret * self`` ==
| ``self * ret`` == ``np.matrix(np.eye(self[0,:].size)`` all return
| ``True``.
|
| Raises
| ------
| numpy.linalg.LinAlgError: Singular matrix
| If `self` is singular.
|
| See Also
| --------
| linalg.inv
|
| Examples
| --------
| >>> m = np.matrix('[1, 2; 3, 4]'); m
| matrix([[1, 2],
| [3, 4]])
| >>> m.getI()
| matrix([[-2. , 1. ],
| [ 1.5, -0.5]])
| >>> m.getI() * m
| matrix([[ 1., 0.], # may vary
| [ 0., 1.]])
|
| getT = T(self)
| Returns the transpose of the matrix.
|
| Does *not* conjugate! For the complex conjugate transpose, use ``.H``.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : matrix object
| The (non-conjugated) transpose of the matrix.
|
| See Also
| --------
| transpose, getH
|
| Examples
| --------
| >>> m = np.matrix('[1, 2; 3, 4]')
| >>> m
| matrix([[1, 2],
| [3, 4]])
| >>> m.getT()
| matrix([[1, 3],
| [2, 4]])
|
| max(self, axis=None, out=None)
| Return the maximum value along an axis.
|
| Parameters
| ----------
| See `amax` for complete descriptions
|
| See Also
| --------
| amax, ndarray.max
|
| Notes
| -----
| This is the same as `ndarray.max`, but returns a `matrix` object
| where `ndarray.max` would return an ndarray.
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.max()
| 11
| >>> x.max(0)
| matrix([[ 8, 9, 10, 11]])
| >>> x.max(1)
| matrix([[ 3],
| [ 7],
| [11]])
|
| mean(self, axis=None, dtype=None, out=None)
| Returns the average of the matrix elements along the given axis.
|
| Refer to `numpy.mean` for full documentation.
|
| See Also
| --------
| numpy.mean
|
| Notes
| -----
| Same as `ndarray.mean` except that, where that returns an `ndarray`,
| this returns a `matrix` object.
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3, 4)))
| >>> x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.mean()
| 5.5
| >>> x.mean(0)
| matrix([[4., 5., 6., 7.]])
| >>> x.mean(1)
| matrix([[ 1.5],
| [ 5.5],
| [ 9.5]])
|
| min(self, axis=None, out=None)
| Return the minimum value along an axis.
|
| Parameters
| ----------
| See `amin` for complete descriptions.
|
| See Also
| --------
| amin, ndarray.min
|
| Notes
| -----
| This is the same as `ndarray.min`, but returns a `matrix` object
| where `ndarray.min` would return an ndarray.
|
| Examples
| --------
| >>> x = -np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, -1, -2, -3],
| [ -4, -5, -6, -7],
| [ -8, -9, -10, -11]])
| >>> x.min()
| -11
| >>> x.min(0)
| matrix([[ -8, -9, -10, -11]])
| >>> x.min(1)
| matrix([[ -3],
| [ -7],
| [-11]])
|
| prod(self, axis=None, dtype=None, out=None)
| Return the product of the array elements over the given axis.
|
| Refer to `prod` for full documentation.
|
| See Also
| --------
| prod, ndarray.prod
|
| Notes
| -----
| Same as `ndarray.prod`, except, where that returns an `ndarray`, this
| returns a `matrix` object instead.
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.prod()
| 0
| >>> x.prod(0)
| matrix([[ 0, 45, 120, 231]])
| >>> x.prod(1)
| matrix([[ 0],
| [ 840],
| [7920]])
|
| ptp(self, axis=None, out=None)
| Peak-to-peak (maximum - minimum) value along the given axis.
|
| Refer to `numpy.ptp` for full documentation.
|
| See Also
| --------
| numpy.ptp
|
| Notes
| -----
| Same as `ndarray.ptp`, except, where that would return an `ndarray` object,
| this returns a `matrix` object.
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.ptp()
| 11
| >>> x.ptp(0)
| matrix([[8, 8, 8, 8]])
| >>> x.ptp(1)
| matrix([[3],
| [3],
| [3]])
|
| ravel(self, order='C')
| Return a flattened matrix.
|
| Refer to `numpy.ravel` for more documentation.
|
| Parameters
| ----------
| order : {'C', 'F', 'A', 'K'}, optional
| The elements of `m` are read using this index order. 'C' means to
| index the elements in C-like order, with the last axis index
| changing fastest, back to the first axis index changing slowest.
| 'F' means to index the elements in Fortran-like index order, with
| the first index changing fastest, and the last index changing
| slowest. Note that the 'C' and 'F' options take no account of the
| memory layout of the underlying array, and only refer to the order
| of axis indexing. 'A' means to read the elements in Fortran-like
| index order if `m` is Fortran *contiguous* in memory, C-like order
| otherwise. 'K' means to read the elements in the order they occur
| in memory, except for reversing the data when strides are negative.
| By default, 'C' index order is used.
|
| Returns
| -------
| ret : matrix
| Return the matrix flattened to shape `(1, N)` where `N`
| is the number of elements in the original matrix.
| A copy is made only if necessary.
|
| See Also
| --------
| matrix.flatten : returns a similar output matrix but always a copy
| matrix.flat : a flat iterator on the array.
| numpy.ravel : related function which returns an ndarray
|
| squeeze(self, axis=None)
| Return a possibly reshaped matrix.
|
| Refer to `numpy.squeeze` for more documentation.
|
| Parameters
| ----------
| axis : None or int or tuple of ints, optional
| Selects a subset of the single-dimensional entries in the shape.
| If an axis is selected with shape entry greater than one,
| an error is raised.
|
| Returns
| -------
| squeezed : matrix
| The matrix, but as a (1, N) matrix if it had shape (N, 1).
|
| See Also
| --------
| numpy.squeeze : related function
|
| Notes
| -----
| If `m` has a single column then that column is returned
| as the single row of a matrix. Otherwise `m` is returned.
| The returned matrix is always either `m` itself or a view into `m`.
| Supplying an axis keyword argument will not affect the returned matrix
| but it may cause an error to be raised.
|
| Examples
| --------
| >>> c = np.matrix([[1], [2]])
| >>> c
| matrix([[1],
| [2]])
| >>> c.squeeze()
| matrix([[1, 2]])
| >>> r = c.T
| >>> r
| matrix([[1, 2]])
| >>> r.squeeze()
| matrix([[1, 2]])
| >>> m = np.matrix([[1, 2], [3, 4]])
| >>> m.squeeze()
| matrix([[1, 2],
| [3, 4]])
|
| std(self, axis=None, dtype=None, out=None, ddof=0)
| Return the standard deviation of the array elements along the given axis.
|
| Refer to `numpy.std` for full documentation.
|
| See Also
| --------
| numpy.std
|
| Notes
| -----
| This is the same as `ndarray.std`, except that where an `ndarray` would
| be returned, a `matrix` object is returned instead.
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3, 4)))
| >>> x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.std()
| 3.4520525295346629 # may vary
| >>> x.std(0)
| matrix([[ 3.26598632, 3.26598632, 3.26598632, 3.26598632]]) # may vary
| >>> x.std(1)
| matrix([[ 1.11803399],
| [ 1.11803399],
| [ 1.11803399]])
|
| sum(self, axis=None, dtype=None, out=None)
| Returns the sum of the matrix elements, along the given axis.
|
| Refer to `numpy.sum` for full documentation.
|
| See Also
| --------
| numpy.sum
|
| Notes
| -----
| This is the same as `ndarray.sum`, except that where an `ndarray` would
| be returned, a `matrix` object is returned instead.
|
| Examples
| --------
| >>> x = np.matrix([[1, 2], [4, 3]])
| >>> x.sum()
| 10
| >>> x.sum(axis=1)
| matrix([[3],
| [7]])
| >>> x.sum(axis=1, dtype='float')
| matrix([[3.],
| [7.]])
| >>> out = np.zeros((2, 1), dtype='float')
| >>> x.sum(axis=1, dtype='float', out=np.asmatrix(out))
| matrix([[3.],
| [7.]])
|
| tolist(self)
| Return the matrix as a (possibly nested) list.
|
| See `ndarray.tolist` for full documentation.
|
| See Also
| --------
| ndarray.tolist
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.tolist()
| [[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11]]
|
| var(self, axis=None, dtype=None, out=None, ddof=0)
| Returns the variance of the matrix elements, along the given axis.
|
| Refer to `numpy.var` for full documentation.
|
| See Also
| --------
| numpy.var
|
| Notes
| -----
| This is the same as `ndarray.var`, except that where an `ndarray` would
| be returned, a `matrix` object is returned instead.
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3, 4)))
| >>> x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.var()
| 11.916666666666666
| >>> x.var(0)
| matrix([[ 10.66666667, 10.66666667, 10.66666667, 10.66666667]]) # may vary
| >>> x.var(1)
| matrix([[1.25],
| [1.25],
| [1.25]])
|
| ----------------------------------------------------------------------
| Static methods defined here:
|
| __new__(subtype, data, dtype=None, copy=True)
| Create and return a new object. See help(type) for accurate signature.
|
| ----------------------------------------------------------------------
| Readonly properties defined here:
|
| A
| Return `self` as an `ndarray` object.
|
| Equivalent to ``np.asarray(self)``.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : ndarray
| `self` as an `ndarray`
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.getA()
| array([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
|
| A1
| Return `self` as a flattened `ndarray`.
|
| Equivalent to ``np.asarray(x).ravel()``
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : ndarray
| `self`, 1-D, as an `ndarray`
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4))); x
| matrix([[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]])
| >>> x.getA1()
| array([ 0, 1, 2, ..., 9, 10, 11])
|
| H
| Returns the (complex) conjugate transpose of `self`.
|
| Equivalent to ``np.transpose(self)`` if `self` is real-valued.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : matrix object
| complex conjugate transpose of `self`
|
| Examples
| --------
| >>> x = np.matrix(np.arange(12).reshape((3,4)))
| >>> z = x - 1j*x; z
| matrix([[ 0. +0.j, 1. -1.j, 2. -2.j, 3. -3.j],
| [ 4. -4.j, 5. -5.j, 6. -6.j, 7. -7.j],
| [ 8. -8.j, 9. -9.j, 10.-10.j, 11.-11.j]])
| >>> z.getH()
| matrix([[ 0. -0.j, 4. +4.j, 8. +8.j],
| [ 1. +1.j, 5. +5.j, 9. +9.j],
| [ 2. +2.j, 6. +6.j, 10.+10.j],
| [ 3. +3.j, 7. +7.j, 11.+11.j]])
|
| I
| Returns the (multiplicative) inverse of invertible `self`.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : matrix object
| If `self` is non-singular, `ret` is such that ``ret * self`` ==
| ``self * ret`` == ``np.matrix(np.eye(self[0,:].size)`` all return
| ``True``.
|
| Raises
| ------
| numpy.linalg.LinAlgError: Singular matrix
| If `self` is singular.
|
| See Also
| --------
| linalg.inv
|
| Examples
| --------
| >>> m = np.matrix('[1, 2; 3, 4]'); m
| matrix([[1, 2],
| [3, 4]])
| >>> m.getI()
| matrix([[-2. , 1. ],
| [ 1.5, -0.5]])
| >>> m.getI() * m
| matrix([[ 1., 0.], # may vary
| [ 0., 1.]])
|
| T
| Returns the transpose of the matrix.
|
| Does *not* conjugate! For the complex conjugate transpose, use ``.H``.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| ret : matrix object
| The (non-conjugated) transpose of the matrix.
|
| See Also
| --------
| transpose, getH
|
| Examples
| --------
| >>> m = np.matrix('[1, 2; 3, 4]')
| >>> m
| matrix([[1, 2],
| [3, 4]])
| >>> m.getT()
| matrix([[1, 3],
| [2, 4]])
|
| ----------------------------------------------------------------------
| Data descriptors defined here:
|
| __dict__
| dictionary for instance variables (if defined)
|
| ----------------------------------------------------------------------
| Data and other attributes defined here:
|
| __array_priority__ = 10.0
|
| ----------------------------------------------------------------------
| Methods inherited from ndarray:
|
| __abs__(self, /)
| abs(self)
|
| __add__(self, value, /)
| Return self+value.
|
| __and__(self, value, /)
| Return self&value.
|
| __array__(...)
| a.__array__(|dtype) -> reference if type unchanged, copy otherwise.
|
| Returns either a new reference to self if dtype is not given or a new array
| of provided data type if dtype is different from the current dtype of the
| array.
|
| __array_function__(...)
|
| __array_prepare__(...)
| a.__array_prepare__(obj) -> Object of same type as ndarray object obj.
|
| __array_ufunc__(...)
|
| __array_wrap__(...)
| a.__array_wrap__(obj) -> Object of same type as ndarray object a.
|
| __bool__(self, /)
| self != 0
|
| __complex__(...)
|
| __contains__(self, key, /)
| Return key in self.
|
| __copy__(...)
| a.__copy__()
|
| Used if :func:`copy.copy` is called on an array. Returns a copy of the array.
|
| Equivalent to ``a.copy(order='K')``.
|
| __deepcopy__(...)
| a.__deepcopy__(memo, /) -> Deep copy of array.
|
| Used if :func:`copy.deepcopy` is called on an array.
|
| __delitem__(self, key, /)
| Delete self[key].
|
| __divmod__(self, value, /)
| Return divmod(self, value).
|
| __eq__(self, value, /)
| Return self==value.
|
| __float__(self, /)
| float(self)
|
| __floordiv__(self, value, /)
| Return self//value.
|
| __format__(...)
| Default object formatter.
|
| __ge__(self, value, /)
| Return self>=value.
|
| __gt__(self, value, /)
| Return self>value.
|
| __iadd__(self, value, /)
| Return self+=value.
|
| __iand__(self, value, /)
| Return self&=value.
|
| __ifloordiv__(self, value, /)
| Return self//=value.
|
| __ilshift__(self, value, /)
| Return self<<=value.
|
| __imatmul__(self, value, /)
| Return self@=value.
|
| __imod__(self, value, /)
| Return self%=value.
|
| __index__(self, /)
| Return self converted to an integer, if self is suitable for use as an index into a list.
|
| __int__(self, /)
| int(self)
|
| __invert__(self, /)
| ~self
|
| __ior__(self, value, /)
| Return self|=value.
|
| __irshift__(self, value, /)
| Return self>>=value.
|
| __isub__(self, value, /)
| Return self-=value.
|
| __iter__(self, /)
| Implement iter(self).
|
| __itruediv__(self, value, /)
| Return self/=value.
|
| __ixor__(self, value, /)
| Return self^=value.
|
| __le__(self, value, /)
| Return self<=value.
|
| __len__(self, /)
| Return len(self).
|
| __lshift__(self, value, /)
| Return self<<value.
|
| __lt__(self, value, /)
| Return self<value.
|
| __matmul__(self, value, /)
| Return self@value.
|
| __mod__(self, value, /)
| Return self%value.
|
| __ne__(self, value, /)
| Return self!=value.
|
| __neg__(self, /)
| -self
|
| __or__(self, value, /)
| Return self|value.
|
| __pos__(self, /)
| +self
|
| __radd__(self, value, /)
| Return value+self.
|
| __rand__(self, value, /)
| Return value&self.
|
| __rdivmod__(self, value, /)
| Return divmod(value, self).
|
| __reduce__(...)
| a.__reduce__()
|
| For pickling.
|
| __reduce_ex__(...)
| Helper for pickle.
|
| __repr__(self, /)
| Return repr(self).
|
| __rfloordiv__(self, value, /)
| Return value//self.
|
| __rlshift__(self, value, /)
| Return value<<self.
|
| __rmatmul__(self, value, /)
| Return value@self.
|
| __rmod__(self, value, /)
| Return value%self.
|
| __ror__(self, value, /)
| Return value|self.
|
| __rrshift__(self, value, /)
| Return value>>self.
|
| __rshift__(self, value, /)
| Return self>>value.
|
| __rsub__(self, value, /)
| Return value-self.
|
| __rtruediv__(self, value, /)
| Return value/self.
|
| __rxor__(self, value, /)
| Return value^self.
|
| __setitem__(self, key, value, /)
| Set self[key] to value.
|
| __setstate__(...)
| a.__setstate__(state, /)
|
| For unpickling.
|
| The `state` argument must be a sequence that contains the following
| elements:
|
| Parameters
| ----------
| version : int
| optional pickle version. If omitted defaults to 0.
| shape : tuple
| dtype : data-type
| isFortran : bool
| rawdata : string or list
| a binary string with the data (or a list if 'a' is an object array)
|
| __sizeof__(...)
| Size of object in memory, in bytes.
|
| __str__(self, /)
| Return str(self).
|
| __sub__(self, value, /)
| Return self-value.
|
| __truediv__(self, value, /)
| Return self/value.
|
| __xor__(self, value, /)
| Return self^value.
|
| argpartition(...)
| a.argpartition(kth, axis=-1, kind='introselect', order=None)
|
| Returns the indices that would partition this array.
|
| Refer to `numpy.argpartition` for full documentation.
|
| .. versionadded:: 1.8.0
|
| See Also
| --------
| numpy.argpartition : equivalent function
|
| argsort(...)
| a.argsort(axis=-1, kind=None, order=None)
|
| Returns the indices that would sort this array.
|
| Refer to `numpy.argsort` for full documentation.
|
| See Also
| --------
| numpy.argsort : equivalent function
|
| astype(...)
| a.astype(dtype, order='K', casting='unsafe', subok=True, copy=True)
|
| Copy of the array, cast to a specified type.
|
| Parameters
| ----------
| dtype : str or dtype
| Typecode or data-type to which the array is cast.
| order : {'C', 'F', 'A', 'K'}, optional
| Controls the memory layout order of the result.
| 'C' means C order, 'F' means Fortran order, 'A'
| means 'F' order if all the arrays are Fortran contiguous,
| 'C' order otherwise, and 'K' means as close to the
| order the array elements appear in memory as possible.
| Default is 'K'.
| casting : {'no', 'equiv', 'safe', 'same_kind', 'unsafe'}, optional
| Controls what kind of data casting may occur. Defaults to 'unsafe'
| for backwards compatibility.
|
| * 'no' means the data types should not be cast at all.
| * 'equiv' means only byte-order changes are allowed.
| * 'safe' means only casts which can preserve values are allowed.
| * 'same_kind' means only safe casts or casts within a kind,
| like float64 to float32, are allowed.
| * 'unsafe' means any data conversions may be done.
| subok : bool, optional
| If True, then sub-classes will be passed-through (default), otherwise
| the returned array will be forced to be a base-class array.
| copy : bool, optional
| By default, astype always returns a newly allocated array. If this
| is set to false, and the `dtype`, `order`, and `subok`
| requirements are satisfied, the input array is returned instead
| of a copy.
|
| Returns
| -------
| arr_t : ndarray
| Unless `copy` is False and the other conditions for returning the input
| array are satisfied (see description for `copy` input parameter), `arr_t`
| is a new array of the same shape as the input array, with dtype, order
| given by `dtype`, `order`.
|
| Notes
| -----
| .. versionchanged:: 1.17.0
| Casting between a simple data type and a structured one is possible only
| for "unsafe" casting. Casting to multiple fields is allowed, but
| casting from multiple fields is not.
|
| .. versionchanged:: 1.9.0
| Casting from numeric to string types in 'safe' casting mode requires
| that the string dtype length is long enough to store the max
| integer/float value converted.
|
| Raises
| ------
| ComplexWarning
| When casting from complex to float or int. To avoid this,
| one should use ``a.real.astype(t)``.
|
| Examples
| --------
| >>> x = np.array([1, 2, 2.5])
| >>> x
| array([1. , 2. , 2.5])
|
| >>> x.astype(int)
| array([1, 2, 2])
|
| byteswap(...)
| a.byteswap(inplace=False)
|
| Swap the bytes of the array elements
|
| Toggle between low-endian and big-endian data representation by
| returning a byteswapped array, optionally swapped in-place.
| Arrays of byte-strings are not swapped. The real and imaginary
| parts of a complex number are swapped individually.
|
| Parameters
| ----------
| inplace : bool, optional
| If ``True``, swap bytes in-place, default is ``False``.
|
| Returns
| -------
| out : ndarray
| The byteswapped array. If `inplace` is ``True``, this is
| a view to self.
|
| Examples
| --------
| >>> A = np.array([1, 256, 8755], dtype=np.int16)
| >>> list(map(hex, A))
| ['0x1', '0x100', '0x2233']
| >>> A.byteswap(inplace=True)
| array([ 256, 1, 13090], dtype=int16)
| >>> list(map(hex, A))
| ['0x100', '0x1', '0x3322']
|
| Arrays of byte-strings are not swapped
|
| >>> A = np.array([b'ceg', b'fac'])
| >>> A.byteswap()
| array([b'ceg', b'fac'], dtype='|S3')
|
| ``A.newbyteorder().byteswap()`` produces an array with the same values
| but different representation in memory
|
| >>> A = np.array([1, 2, 3])
| >>> A.view(np.uint8)
| array([1, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0,
| 0, 0], dtype=uint8)
| >>> A.newbyteorder().byteswap(inplace=True)
| array([1, 2, 3])
| >>> A.view(np.uint8)
| array([0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0,
| 0, 3], dtype=uint8)
|
| choose(...)
| a.choose(choices, out=None, mode='raise')
|
| Use an index array to construct a new array from a set of choices.
|
| Refer to `numpy.choose` for full documentation.
|
| See Also
| --------
| numpy.choose : equivalent function
|
| clip(...)
| a.clip(min=None, max=None, out=None, **kwargs)
|
| Return an array whose values are limited to ``[min, max]``.
| One of max or min must be given.
|
| Refer to `numpy.clip` for full documentation.
|
| See Also
| --------
| numpy.clip : equivalent function
|
| compress(...)
| a.compress(condition, axis=None, out=None)
|
| Return selected slices of this array along given axis.
|
| Refer to `numpy.compress` for full documentation.
|
| See Also
| --------
| numpy.compress : equivalent function
|
| conj(...)
| a.conj()
|
| Complex-conjugate all elements.
|
| Refer to `numpy.conjugate` for full documentation.
|
| See Also
| --------
| numpy.conjugate : equivalent function
|
| conjugate(...)
| a.conjugate()
|
| Return the complex conjugate, element-wise.
|
| Refer to `numpy.conjugate` for full documentation.
|
| See Also
| --------
| numpy.conjugate : equivalent function
|
| copy(...)
| a.copy(order='C')
|
| Return a copy of the array.
|
| Parameters
| ----------
| order : {'C', 'F', 'A', 'K'}, optional
| Controls the memory layout of the copy. 'C' means C-order,
| 'F' means F-order, 'A' means 'F' if `a` is Fortran contiguous,
| 'C' otherwise. 'K' means match the layout of `a` as closely
| as possible. (Note that this function and :func:`numpy.copy` are very
| similar, but have different default values for their order=
| arguments.)
|
| See also
| --------
| numpy.copy
| numpy.copyto
|
| Examples
| --------
| >>> x = np.array([[1,2,3],[4,5,6]], order='F')
|
| >>> y = x.copy()
|
| >>> x.fill(0)
|
| >>> x
| array([[0, 0, 0],
| [0, 0, 0]])
|
| >>> y
| array([[1, 2, 3],
| [4, 5, 6]])
|
| >>> y.flags['C_CONTIGUOUS']
| True
|
| cumprod(...)
| a.cumprod(axis=None, dtype=None, out=None)
|
| Return the cumulative product of the elements along the given axis.
|
| Refer to `numpy.cumprod` for full documentation.
|
| See Also
| --------
| numpy.cumprod : equivalent function
|
| cumsum(...)
| a.cumsum(axis=None, dtype=None, out=None)
|
| Return the cumulative sum of the elements along the given axis.
|
| Refer to `numpy.cumsum` for full documentation.
|
| See Also
| --------
| numpy.cumsum : equivalent function
|
| diagonal(...)
| a.diagonal(offset=0, axis1=0, axis2=1)
|
| Return specified diagonals. In NumPy 1.9 the returned array is a
| read-only view instead of a copy as in previous NumPy versions. In
| a future version the read-only restriction will be removed.
|
| Refer to :func:`numpy.diagonal` for full documentation.
|
| See Also
| --------
| numpy.diagonal : equivalent function
|
| dot(...)
| a.dot(b, out=None)
|
| Dot product of two arrays.
|
| Refer to `numpy.dot` for full documentation.
|
| See Also
| --------
| numpy.dot : equivalent function
|
| Examples
| --------
| >>> a = np.eye(2)
| >>> b = np.ones((2, 2)) * 2
| >>> a.dot(b)
| array([[2., 2.],
| [2., 2.]])
|
| This array method can be conveniently chained:
|
| >>> a.dot(b).dot(b)
| array([[8., 8.],
| [8., 8.]])
|
| dump(...)
| a.dump(file)
|
| Dump a pickle of the array to the specified file.
| The array can be read back with pickle.load or numpy.load.
|
| Parameters
| ----------
| file : str or Path
| A string naming the dump file.
|
| .. versionchanged:: 1.17.0
| `pathlib.Path` objects are now accepted.
|
| dumps(...)
| a.dumps()
|
| Returns the pickle of the array as a string.
| pickle.loads or numpy.loads will convert the string back to an array.
|
| Parameters
| ----------
| None
|
| fill(...)
| a.fill(value)
|
| Fill the array with a scalar value.
|
| Parameters
| ----------
| value : scalar
| All elements of `a` will be assigned this value.
|
| Examples
| --------
| >>> a = np.array([1, 2])
| >>> a.fill(0)
| >>> a
| array([0, 0])
| >>> a = np.empty(2)
| >>> a.fill(1)
| >>> a
| array([1., 1.])
|
| getfield(...)
| a.getfield(dtype, offset=0)
|
| Returns a field of the given array as a certain type.
|
| A field is a view of the array data with a given data-type. The values in
| the view are determined by the given type and the offset into the current
| array in bytes. The offset needs to be such that the view dtype fits in the
| array dtype; for example an array of dtype complex128 has 16-byte elements.
| If taking a view with a 32-bit integer (4 bytes), the offset needs to be
| between 0 and 12 bytes.
|
| Parameters
| ----------
| dtype : str or dtype
| The data type of the view. The dtype size of the view can not be larger
| than that of the array itself.
| offset : int
| Number of bytes to skip before beginning the element view.
|
| Examples
| --------
| >>> x = np.diag([1.+1.j]*2)
| >>> x[1, 1] = 2 + 4.j
| >>> x
| array([[1.+1.j, 0.+0.j],
| [0.+0.j, 2.+4.j]])
| >>> x.getfield(np.float64)
| array([[1., 0.],
| [0., 2.]])
|
| By choosing an offset of 8 bytes we can select the complex part of the
| array for our view:
|
| >>> x.getfield(np.float64, offset=8)
| array([[1., 0.],
| [0., 4.]])
|
| item(...)
| a.item(*args)
|
| Copy an element of an array to a standard Python scalar and return it.
|
| Parameters
| ----------
| \*args : Arguments (variable number and type)
|
| * none: in this case, the method only works for arrays
| with one element (`a.size == 1`), which element is
| copied into a standard Python scalar object and returned.
|
| * int_type: this argument is interpreted as a flat index into
| the array, specifying which element to copy and return.
|
| * tuple of int_types: functions as does a single int_type argument,
| except that the argument is interpreted as an nd-index into the
| array.
|
| Returns
| -------
| z : Standard Python scalar object
| A copy of the specified element of the array as a suitable
| Python scalar
|
| Notes
| -----
| When the data type of `a` is longdouble or clongdouble, item() returns
| a scalar array object because there is no available Python scalar that
| would not lose information. Void arrays return a buffer object for item(),
| unless fields are defined, in which case a tuple is returned.
|
| `item` is very similar to a[args], except, instead of an array scalar,
| a standard Python scalar is returned. This can be useful for speeding up
| access to elements of the array and doing arithmetic on elements of the
| array using Python's optimized math.
|
| Examples
| --------
| >>> np.random.seed(123)
| >>> x = np.random.randint(9, size=(3, 3))
| >>> x
| array([[2, 2, 6],
| [1, 3, 6],
| [1, 0, 1]])
| >>> x.item(3)
| 1
| >>> x.item(7)
| 0
| >>> x.item((0, 1))
| 2
| >>> x.item((2, 2))
| 1
|
| itemset(...)
| a.itemset(*args)
|
| Insert scalar into an array (scalar is cast to array's dtype, if possible)
|
| There must be at least 1 argument, and define the last argument
| as *item*. Then, ``a.itemset(*args)`` is equivalent to but faster
| than ``a[args] = item``. The item should be a scalar value and `args`
| must select a single item in the array `a`.
|
| Parameters
| ----------
| \*args : Arguments
| If one argument: a scalar, only used in case `a` is of size 1.
| If two arguments: the last argument is the value to be set
| and must be a scalar, the first argument specifies a single array
| element location. It is either an int or a tuple.
|
| Notes
| -----
| Compared to indexing syntax, `itemset` provides some speed increase
| for placing a scalar into a particular location in an `ndarray`,
| if you must do this. However, generally this is discouraged:
| among other problems, it complicates the appearance of the code.
| Also, when using `itemset` (and `item`) inside a loop, be sure
| to assign the methods to a local variable to avoid the attribute
| look-up at each loop iteration.
|
| Examples
| --------
| >>> np.random.seed(123)
| >>> x = np.random.randint(9, size=(3, 3))
| >>> x
| array([[2, 2, 6],
| [1, 3, 6],
| [1, 0, 1]])
| >>> x.itemset(4, 0)
| >>> x.itemset((2, 2), 9)
| >>> x
| array([[2, 2, 6],
| [1, 0, 6],
| [1, 0, 9]])
|
| newbyteorder(...)
| arr.newbyteorder(new_order='S')
|
| Return the array with the same data viewed with a different byte order.
|
| Equivalent to::
|
| arr.view(arr.dtype.newbytorder(new_order))
|
| Changes are also made in all fields and sub-arrays of the array data
| type.
|
|
|
| Parameters
| ----------
| new_order : string, optional
| Byte order to force; a value from the byte order specifications
| below. `new_order` codes can be any of:
|
| * 'S' - swap dtype from current to opposite endian
| * {'<', 'L'} - little endian
| * {'>', 'B'} - big endian
| * {'=', 'N'} - native order
| * {'|', 'I'} - ignore (no change to byte order)
|
| The default value ('S') results in swapping the current
| byte order. The code does a case-insensitive check on the first
| letter of `new_order` for the alternatives above. For example,
| any of 'B' or 'b' or 'biggish' are valid to specify big-endian.
|
|
| Returns
| -------
| new_arr : array
| New array object with the dtype reflecting given change to the
| byte order.
|
| nonzero(...)
| a.nonzero()
|
| Return the indices of the elements that are non-zero.
|
| Refer to `numpy.nonzero` for full documentation.
|
| See Also
| --------
| numpy.nonzero : equivalent function
|
| partition(...)
| a.partition(kth, axis=-1, kind='introselect', order=None)
|
| Rearranges the elements in the array in such a way that the value of the
| element in kth position is in the position it would be in a sorted array.
| All elements smaller than the kth element are moved before this element and
| all equal or greater are moved behind it. The ordering of the elements in
| the two partitions is undefined.
|
| .. versionadded:: 1.8.0
|
| Parameters
| ----------
| kth : int or sequence of ints
| Element index to partition by. The kth element value will be in its
| final sorted position and all smaller elements will be moved before it
| and all equal or greater elements behind it.
| The order of all elements in the partitions is undefined.
| If provided with a sequence of kth it will partition all elements
| indexed by kth of them into their sorted position at once.
| axis : int, optional
| Axis along which to sort. Default is -1, which means sort along the
| last axis.
| kind : {'introselect'}, optional
| Selection algorithm. Default is 'introselect'.
| order : str or list of str, optional
| When `a` is an array with fields defined, this argument specifies
| which fields to compare first, second, etc. A single field can
| be specified as a string, and not all fields need to be specified,
| but unspecified fields will still be used, in the order in which
| they come up in the dtype, to break ties.
|
| See Also
| --------
| numpy.partition : Return a parititioned copy of an array.
| argpartition : Indirect partition.
| sort : Full sort.
|
| Notes
| -----
| See ``np.partition`` for notes on the different algorithms.
|
| Examples
| --------
| >>> a = np.array([3, 4, 2, 1])
| >>> a.partition(3)
| >>> a
| array([2, 1, 3, 4])
|
| >>> a.partition((1, 3))
| >>> a
| array([1, 2, 3, 4])
|
| put(...)
| a.put(indices, values, mode='raise')
|
| Set ``a.flat[n] = values[n]`` for all `n` in indices.
|
| Refer to `numpy.put` for full documentation.
|
| See Also
| --------
| numpy.put : equivalent function
|
| repeat(...)
| a.repeat(repeats, axis=None)
|
| Repeat elements of an array.
|
| Refer to `numpy.repeat` for full documentation.
|
| See Also
| --------
| numpy.repeat : equivalent function
|
| reshape(...)
| a.reshape(shape, order='C')
|
| Returns an array containing the same data with a new shape.
|
| Refer to `numpy.reshape` for full documentation.
|
| See Also
| --------
| numpy.reshape : equivalent function
|
| Notes
| -----
| Unlike the free function `numpy.reshape`, this method on `ndarray` allows
| the elements of the shape parameter to be passed in as separate arguments.
| For example, ``a.reshape(10, 11)`` is equivalent to
| ``a.reshape((10, 11))``.
|
| resize(...)
| a.resize(new_shape, refcheck=True)
|
| Change shape and size of array in-place.
|
| Parameters
| ----------
| new_shape : tuple of ints, or `n` ints
| Shape of resized array.
| refcheck : bool, optional
| If False, reference count will not be checked. Default is True.
|
| Returns
| -------
| None
|
| Raises
| ------
| ValueError
| If `a` does not own its own data or references or views to it exist,
| and the data memory must be changed.
| PyPy only: will always raise if the data memory must be changed, since
| there is no reliable way to determine if references or views to it
| exist.
|
| SystemError
| If the `order` keyword argument is specified. This behaviour is a
| bug in NumPy.
|
| See Also
| --------
| resize : Return a new array with the specified shape.
|
| Notes
| -----
| This reallocates space for the data area if necessary.
|
| Only contiguous arrays (data elements consecutive in memory) can be
| resized.
|
| The purpose of the reference count check is to make sure you
| do not use this array as a buffer for another Python object and then
| reallocate the memory. However, reference counts can increase in
| other ways so if you are sure that you have not shared the memory
| for this array with another Python object, then you may safely set
| `refcheck` to False.
|
| Examples
| --------
| Shrinking an array: array is flattened (in the order that the data are
| stored in memory), resized, and reshaped:
|
| >>> a = np.array([[0, 1], [2, 3]], order='C')
| >>> a.resize((2, 1))
| >>> a
| array([[0],
| [1]])
|
| >>> a = np.array([[0, 1], [2, 3]], order='F')
| >>> a.resize((2, 1))
| >>> a
| array([[0],
| [2]])
|
| Enlarging an array: as above, but missing entries are filled with zeros:
|
| >>> b = np.array([[0, 1], [2, 3]])
| >>> b.resize(2, 3) # new_shape parameter doesn't have to be a tuple
| >>> b
| array([[0, 1, 2],
| [3, 0, 0]])
|
| Referencing an array prevents resizing...
|
| >>> c = a
| >>> a.resize((1, 1))
| Traceback (most recent call last):
| ...
| ValueError: cannot resize an array that references or is referenced ...
|
| Unless `refcheck` is False:
|
| >>> a.resize((1, 1), refcheck=False)
| >>> a
| array([[0]])
| >>> c
| array([[0]])
|
| round(...)
| a.round(decimals=0, out=None)
|
| Return `a` with each element rounded to the given number of decimals.
|
| Refer to `numpy.around` for full documentation.
|
| See Also
| --------
| numpy.around : equivalent function
|
| searchsorted(...)
| a.searchsorted(v, side='left', sorter=None)
|
| Find indices where elements of v should be inserted in a to maintain order.
|
| For full documentation, see `numpy.searchsorted`
|
| See Also
| --------
| numpy.searchsorted : equivalent function
|
| setfield(...)
| a.setfield(val, dtype, offset=0)
|
| Put a value into a specified place in a field defined by a data-type.
|
| Place `val` into `a`'s field defined by `dtype` and beginning `offset`
| bytes into the field.
|
| Parameters
| ----------
| val : object
| Value to be placed in field.
| dtype : dtype object
| Data-type of the field in which to place `val`.
| offset : int, optional
| The number of bytes into the field at which to place `val`.
|
| Returns
| -------
| None
|
| See Also
| --------
| getfield
|
| Examples
| --------
| >>> x = np.eye(3)
| >>> x.getfield(np.float64)
| array([[1., 0., 0.],
| [0., 1., 0.],
| [0., 0., 1.]])
| >>> x.setfield(3, np.int32)
| >>> x.getfield(np.int32)
| array([[3, 3, 3],
| [3, 3, 3],
| [3, 3, 3]], dtype=int32)
| >>> x
| array([[1.0e+000, 1.5e-323, 1.5e-323],
| [1.5e-323, 1.0e+000, 1.5e-323],
| [1.5e-323, 1.5e-323, 1.0e+000]])
| >>> x.setfield(np.eye(3), np.int32)
| >>> x
| array([[1., 0., 0.],
| [0., 1., 0.],
| [0., 0., 1.]])
|
| setflags(...)
| a.setflags(write=None, align=None, uic=None)
|
| Set array flags WRITEABLE, ALIGNED, (WRITEBACKIFCOPY and UPDATEIFCOPY),
| respectively.
|
| These Boolean-valued flags affect how numpy interprets the memory
| area used by `a` (see Notes below). The ALIGNED flag can only
| be set to True if the data is actually aligned according to the type.
| The WRITEBACKIFCOPY and (deprecated) UPDATEIFCOPY flags can never be set
| to True. The flag WRITEABLE can only be set to True if the array owns its
| own memory, or the ultimate owner of the memory exposes a writeable buffer
| interface, or is a string. (The exception for string is made so that
| unpickling can be done without copying memory.)
|
| Parameters
| ----------
| write : bool, optional
| Describes whether or not `a` can be written to.
| align : bool, optional
| Describes whether or not `a` is aligned properly for its type.
| uic : bool, optional
| Describes whether or not `a` is a copy of another "base" array.
|
| Notes
| -----
| Array flags provide information about how the memory area used
| for the array is to be interpreted. There are 7 Boolean flags
| in use, only four of which can be changed by the user:
| WRITEBACKIFCOPY, UPDATEIFCOPY, WRITEABLE, and ALIGNED.
|
| WRITEABLE (W) the data area can be written to;
|
| ALIGNED (A) the data and strides are aligned appropriately for the hardware
| (as determined by the compiler);
|
| UPDATEIFCOPY (U) (deprecated), replaced by WRITEBACKIFCOPY;
|
| WRITEBACKIFCOPY (X) this array is a copy of some other array (referenced
| by .base). When the C-API function PyArray_ResolveWritebackIfCopy is
| called, the base array will be updated with the contents of this array.
|
| All flags can be accessed using the single (upper case) letter as well
| as the full name.
|
| Examples
| --------
| >>> y = np.array([[3, 1, 7],
| ... [2, 0, 0],
| ... [8, 5, 9]])
| >>> y
| array([[3, 1, 7],
| [2, 0, 0],
| [8, 5, 9]])
| >>> y.flags
| C_CONTIGUOUS : True
| F_CONTIGUOUS : False
| OWNDATA : True
| WRITEABLE : True
| ALIGNED : True
| WRITEBACKIFCOPY : False
| UPDATEIFCOPY : False
| >>> y.setflags(write=0, align=0)
| >>> y.flags
| C_CONTIGUOUS : True
| F_CONTIGUOUS : False
| OWNDATA : True
| WRITEABLE : False
| ALIGNED : False
| WRITEBACKIFCOPY : False
| UPDATEIFCOPY : False
| >>> y.setflags(uic=1)
| Traceback (most recent call last):
| File "<stdin>", line 1, in <module>
| ValueError: cannot set WRITEBACKIFCOPY flag to True
|
| sort(...)
| a.sort(axis=-1, kind=None, order=None)
|
| Sort an array in-place. Refer to `numpy.sort` for full documentation.
|
| Parameters
| ----------
| axis : int, optional
| Axis along which to sort. Default is -1, which means sort along the
| last axis.
| kind : {'quicksort', 'mergesort', 'heapsort', 'stable'}, optional
| Sorting algorithm. The default is 'quicksort'. Note that both 'stable'
| and 'mergesort' use timsort under the covers and, in general, the
| actual implementation will vary with datatype. The 'mergesort' option
| is retained for backwards compatibility.
|
| .. versionchanged:: 1.15.0.
| The 'stable' option was added.
|
| order : str or list of str, optional
| When `a` is an array with fields defined, this argument specifies
| which fields to compare first, second, etc. A single field can
| be specified as a string, and not all fields need be specified,
| but unspecified fields will still be used, in the order in which
| they come up in the dtype, to break ties.
|
| See Also
| --------
| numpy.sort : Return a sorted copy of an array.
| numpy.argsort : Indirect sort.
| numpy.lexsort : Indirect stable sort on multiple keys.
| numpy.searchsorted : Find elements in sorted array.
| numpy.partition: Partial sort.
|
| Notes
| -----
| See `numpy.sort` for notes on the different sorting algorithms.
|
| Examples
| --------
| >>> a = np.array([[1,4], [3,1]])
| >>> a.sort(axis=1)
| >>> a
| array([[1, 4],
| [1, 3]])
| >>> a.sort(axis=0)
| >>> a
| array([[1, 3],
| [1, 4]])
|
| Use the `order` keyword to specify a field to use when sorting a
| structured array:
|
| >>> a = np.array([('a', 2), ('c', 1)], dtype=[('x', 'S1'), ('y', int)])
| >>> a.sort(order='y')
| >>> a
| array([(b'c', 1), (b'a', 2)],
| dtype=[('x', 'S1'), ('y', '<i8')])
|
| swapaxes(...)
| a.swapaxes(axis1, axis2)
|
| Return a view of the array with `axis1` and `axis2` interchanged.
|
| Refer to `numpy.swapaxes` for full documentation.
|
| See Also
| --------
| numpy.swapaxes : equivalent function
|
| take(...)
| a.take(indices, axis=None, out=None, mode='raise')
|
| Return an array formed from the elements of `a` at the given indices.
|
| Refer to `numpy.take` for full documentation.
|
| See Also
| --------
| numpy.take : equivalent function
|
| tobytes(...)
| a.tobytes(order='C')
|
| Construct Python bytes containing the raw data bytes in the array.
|
| Constructs Python bytes showing a copy of the raw contents of
| data memory. The bytes object can be produced in either 'C' or 'Fortran',
| or 'Any' order (the default is 'C'-order). 'Any' order means C-order
| unless the F_CONTIGUOUS flag in the array is set, in which case it
| means 'Fortran' order.
|
| .. versionadded:: 1.9.0
|
| Parameters
| ----------
| order : {'C', 'F', None}, optional
| Order of the data for multidimensional arrays:
| C, Fortran, or the same as for the original array.
|
| Returns
| -------
| s : bytes
| Python bytes exhibiting a copy of `a`'s raw data.
|
| Examples
| --------
| >>> x = np.array([[0, 1], [2, 3]], dtype='<u2')
| >>> x.tobytes()
| b'\x00\x00\x01\x00\x02\x00\x03\x00'
| >>> x.tobytes('C') == x.tobytes()
| True
| >>> x.tobytes('F')
| b'\x00\x00\x02\x00\x01\x00\x03\x00'
|
| tofile(...)
| a.tofile(fid, sep="", format="%s")
|
| Write array to a file as text or binary (default).
|
| Data is always written in 'C' order, independent of the order of `a`.
| The data produced by this method can be recovered using the function
| fromfile().
|
| Parameters
| ----------
| fid : file or str or Path
| An open file object, or a string containing a filename.
|
| .. versionchanged:: 1.17.0
| `pathlib.Path` objects are now accepted.
|
| sep : str
| Separator between array items for text output.
| If "" (empty), a binary file is written, equivalent to
| ``file.write(a.tobytes())``.
| format : str
| Format string for text file output.
| Each entry in the array is formatted to text by first converting
| it to the closest Python type, and then using "format" % item.
|
| Notes
| -----
| This is a convenience function for quick storage of array data.
| Information on endianness and precision is lost, so this method is not a
| good choice for files intended to archive data or transport data between
| machines with different endianness. Some of these problems can be overcome
| by outputting the data as text files, at the expense of speed and file
| size.
|
| When fid is a file object, array contents are directly written to the
| file, bypassing the file object's ``write`` method. As a result, tofile
| cannot be used with files objects supporting compression (e.g., GzipFile)
| or file-like objects that do not support ``fileno()`` (e.g., BytesIO).
|
| tostring(...)
| a.tostring(order='C')
|
| Construct Python bytes containing the raw data bytes in the array.
|
| Constructs Python bytes showing a copy of the raw contents of
| data memory. The bytes object can be produced in either 'C' or 'Fortran',
| or 'Any' order (the default is 'C'-order). 'Any' order means C-order
| unless the F_CONTIGUOUS flag in the array is set, in which case it
| means 'Fortran' order.
|
| This function is a compatibility alias for tobytes. Despite its name it returns bytes not strings.
|
| Parameters
| ----------
| order : {'C', 'F', None}, optional
| Order of the data for multidimensional arrays:
| C, Fortran, or the same as for the original array.
|
| Returns
| -------
| s : bytes
| Python bytes exhibiting a copy of `a`'s raw data.
|
| Examples
| --------
| >>> x = np.array([[0, 1], [2, 3]], dtype='<u2')
| >>> x.tobytes()
| b'\x00\x00\x01\x00\x02\x00\x03\x00'
| >>> x.tobytes('C') == x.tobytes()
| True
| >>> x.tobytes('F')
| b'\x00\x00\x02\x00\x01\x00\x03\x00'
|
| trace(...)
| a.trace(offset=0, axis1=0, axis2=1, dtype=None, out=None)
|
| Return the sum along diagonals of the array.
|
| Refer to `numpy.trace` for full documentation.
|
| See Also
| --------
| numpy.trace : equivalent function
|
| transpose(...)
| a.transpose(*axes)
|
| Returns a view of the array with axes transposed.
|
| For a 1-D array this has no effect, as a transposed vector is simply the
| same vector. To convert a 1-D array into a 2D column vector, an additional
| dimension must be added. `np.atleast2d(a).T` achieves this, as does
| `a[:, np.newaxis]`.
| For a 2-D array, this is a standard matrix transpose.
| For an n-D array, if axes are given, their order indicates how the
| axes are permuted (see Examples). If axes are not provided and
| ``a.shape = (i[0], i[1], ... i[n-2], i[n-1])``, then
| ``a.transpose().shape = (i[n-1], i[n-2], ... i[1], i[0])``.
|
| Parameters
| ----------
| axes : None, tuple of ints, or `n` ints
|
| * None or no argument: reverses the order of the axes.
|
| * tuple of ints: `i` in the `j`-th place in the tuple means `a`'s
| `i`-th axis becomes `a.transpose()`'s `j`-th axis.
|
| * `n` ints: same as an n-tuple of the same ints (this form is
| intended simply as a "convenience" alternative to the tuple form)
|
| Returns
| -------
| out : ndarray
| View of `a`, with axes suitably permuted.
|
| See Also
| --------
| ndarray.T : Array property returning the array transposed.
| ndarray.reshape : Give a new shape to an array without changing its data.
|
| Examples
| --------
| >>> a = np.array([[1, 2], [3, 4]])
| >>> a
| array([[1, 2],
| [3, 4]])
| >>> a.transpose()
| array([[1, 3],
| [2, 4]])
| >>> a.transpose((1, 0))
| array([[1, 3],
| [2, 4]])
| >>> a.transpose(1, 0)
| array([[1, 3],
| [2, 4]])
|
| view(...)
| a.view(dtype=None, type=None)
|
| New view of array with the same data.
|
| Parameters
| ----------
| dtype : data-type or ndarray sub-class, optional
| Data-type descriptor of the returned view, e.g., float32 or int16. The
| default, None, results in the view having the same data-type as `a`.
| This argument can also be specified as an ndarray sub-class, which
| then specifies the type of the returned object (this is equivalent to
| setting the ``type`` parameter).
| type : Python type, optional
| Type of the returned view, e.g., ndarray or matrix. Again, the
| default None results in type preservation.
|
| Notes
| -----
| ``a.view()`` is used two different ways:
|
| ``a.view(some_dtype)`` or ``a.view(dtype=some_dtype)`` constructs a view
| of the array's memory with a different data-type. This can cause a
| reinterpretation of the bytes of memory.
|
| ``a.view(ndarray_subclass)`` or ``a.view(type=ndarray_subclass)`` just
| returns an instance of `ndarray_subclass` that looks at the same array
| (same shape, dtype, etc.) This does not cause a reinterpretation of the
| memory.
|
| For ``a.view(some_dtype)``, if ``some_dtype`` has a different number of
| bytes per entry than the previous dtype (for example, converting a
| regular array to a structured array), then the behavior of the view
| cannot be predicted just from the superficial appearance of ``a`` (shown
| by ``print(a)``). It also depends on exactly how ``a`` is stored in
| memory. Therefore if ``a`` is C-ordered versus fortran-ordered, versus
| defined as a slice or transpose, etc., the view may give different
| results.
|
|
| Examples
| --------
| >>> x = np.array([(1, 2)], dtype=[('a', np.int8), ('b', np.int8)])
|
| Viewing array data using a different type and dtype:
|
| >>> y = x.view(dtype=np.int16, type=np.matrix)
| >>> y
| matrix([[513]], dtype=int16)
| >>> print(type(y))
| <class 'numpy.matrix'>
|
| Creating a view on a structured array so it can be used in calculations
|
| >>> x = np.array([(1, 2),(3,4)], dtype=[('a', np.int8), ('b', np.int8)])
| >>> xv = x.view(dtype=np.int8).reshape(-1,2)
| >>> xv
| array([[1, 2],
| [3, 4]], dtype=int8)
| >>> xv.mean(0)
| array([2., 3.])
|
| Making changes to the view changes the underlying array
|
| >>> xv[0,1] = 20
| >>> x
| array([(1, 20), (3, 4)], dtype=[('a', 'i1'), ('b', 'i1')])
|
| Using a view to convert an array to a recarray:
|
| >>> z = x.view(np.recarray)
| >>> z.a
| array([1, 3], dtype=int8)
|
| Views share data:
|
| >>> x[0] = (9, 10)
| >>> z[0]
| (9, 10)
|
| Views that change the dtype size (bytes per entry) should normally be
| avoided on arrays defined by slices, transposes, fortran-ordering, etc.:
|
| >>> x = np.array([[1,2,3],[4,5,6]], dtype=np.int16)
| >>> y = x[:, 0:2]
| >>> y
| array([[1, 2],
| [4, 5]], dtype=int16)
| >>> y.view(dtype=[('width', np.int16), ('length', np.int16)])
| Traceback (most recent call last):
| ...
| ValueError: To change to a dtype of a different size, the array must be C-contiguous
| >>> z = y.copy()
| >>> z.view(dtype=[('width', np.int16), ('length', np.int16)])
| array([[(1, 2)],
| [(4, 5)]], dtype=[('width', '<i2'), ('length', '<i2')])
|
| ----------------------------------------------------------------------
| Data descriptors inherited from ndarray:
|
| __array_interface__
| Array protocol: Python side.
|
| __array_struct__
| Array protocol: C-struct side.
|
| base
| Base object if memory is from some other object.
|
| Examples
| --------
| The base of an array that owns its memory is None:
|
| >>> x = np.array([1,2,3,4])
| >>> x.base is None
| True
|
| Slicing creates a view, whose memory is shared with x:
|
| >>> y = x[2:]
| >>> y.base is x
| True
|
| ctypes
| An object to simplify the interaction of the array with the ctypes
| module.
|
| This attribute creates an object that makes it easier to use arrays
| when calling shared libraries with the ctypes module. The returned
| object has, among others, data, shape, and strides attributes (see
| Notes below) which themselves return ctypes objects that can be used
| as arguments to a shared library.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| c : Python object
| Possessing attributes data, shape, strides, etc.
|
| See Also
| --------
| numpy.ctypeslib
|
| Notes
| -----
| Below are the public attributes of this object which were documented
| in "Guide to NumPy" (we have omitted undocumented public attributes,
| as well as documented private attributes):
|
| .. autoattribute:: numpy.core._internal._ctypes.data
| :noindex:
|
| .. autoattribute:: numpy.core._internal._ctypes.shape
| :noindex:
|
| .. autoattribute:: numpy.core._internal._ctypes.strides
| :noindex:
|
| .. automethod:: numpy.core._internal._ctypes.data_as
| :noindex:
|
| .. automethod:: numpy.core._internal._ctypes.shape_as
| :noindex:
|
| .. automethod:: numpy.core._internal._ctypes.strides_as
| :noindex:
|
| If the ctypes module is not available, then the ctypes attribute
| of array objects still returns something useful, but ctypes objects
| are not returned and errors may be raised instead. In particular,
| the object will still have the ``as_parameter`` attribute which will
| return an integer equal to the data attribute.
|
| Examples
| --------
| >>> import ctypes
| >>> x
| array([[0, 1],
| [2, 3]])
| >>> x.ctypes.data
| 30439712
| >>> x.ctypes.data_as(ctypes.POINTER(ctypes.c_long))
| <ctypes.LP_c_long object at 0x01F01300>
| >>> x.ctypes.data_as(ctypes.POINTER(ctypes.c_long)).contents
| c_long(0)
| >>> x.ctypes.data_as(ctypes.POINTER(ctypes.c_longlong)).contents
| c_longlong(4294967296L)
| >>> x.ctypes.shape
| <numpy.core._internal.c_long_Array_2 object at 0x01FFD580>
| >>> x.ctypes.shape_as(ctypes.c_long)
| <numpy.core._internal.c_long_Array_2 object at 0x01FCE620>
| >>> x.ctypes.strides
| <numpy.core._internal.c_long_Array_2 object at 0x01FCE620>
| >>> x.ctypes.strides_as(ctypes.c_longlong)
| <numpy.core._internal.c_longlong_Array_2 object at 0x01F01300>
|
| data
| Python buffer object pointing to the start of the array's data.
|
| dtype
| Data-type of the array's elements.
|
| Parameters
| ----------
| None
|
| Returns
| -------
| d : numpy dtype object
|
| See Also
| --------
| numpy.dtype
|
| Examples
| --------
| >>> x
| array([[0, 1],
| [2, 3]])
| >>> x.dtype
| dtype('int32')
| >>> type(x.dtype)
| <type 'numpy.dtype'>
|
| flags
| Information about the memory layout of the array.
|
| Attributes
| ----------
| C_CONTIGUOUS (C)
| The data is in a single, C-style contiguous segment.
| F_CONTIGUOUS (F)
| The data is in a single, Fortran-style contiguous segment.
| OWNDATA (O)
| The array owns the memory it uses or borrows it from another object.
| WRITEABLE (W)
| The data area can be written to. Setting this to False locks
| the data, making it read-only. A view (slice, etc.) inherits WRITEABLE
| from its base array at creation time, but a view of a writeable
| array may be subsequently locked while the base array remains writeable.
| (The opposite is not true, in that a view of a locked array may not
| be made writeable. However, currently, locking a base object does not
| lock any views that already reference it, so under that circumstance it
| is possible to alter the contents of a locked array via a previously
| created writeable view onto it.) Attempting to change a non-writeable
| array raises a RuntimeError exception.
| ALIGNED (A)
| The data and all elements are aligned appropriately for the hardware.
| WRITEBACKIFCOPY (X)
| This array is a copy of some other array. The C-API function
| PyArray_ResolveWritebackIfCopy must be called before deallocating
| to the base array will be updated with the contents of this array.
| UPDATEIFCOPY (U)
| (Deprecated, use WRITEBACKIFCOPY) This array is a copy of some other array.
| When this array is
| deallocated, the base array will be updated with the contents of
| this array.
| FNC
| F_CONTIGUOUS and not C_CONTIGUOUS.
| FORC
| F_CONTIGUOUS or C_CONTIGUOUS (one-segment test).
| BEHAVED (B)
| ALIGNED and WRITEABLE.
| CARRAY (CA)
| BEHAVED and C_CONTIGUOUS.
| FARRAY (FA)
| BEHAVED and F_CONTIGUOUS and not C_CONTIGUOUS.
|
| Notes
| -----
| The `flags` object can be accessed dictionary-like (as in ``a.flags['WRITEABLE']``),
| or by using lowercased attribute names (as in ``a.flags.writeable``). Short flag
| names are only supported in dictionary access.
|
| Only the WRITEBACKIFCOPY, UPDATEIFCOPY, WRITEABLE, and ALIGNED flags can be
| changed by the user, via direct assignment to the attribute or dictionary
| entry, or by calling `ndarray.setflags`.
|
| The array flags cannot be set arbitrarily:
|
| - UPDATEIFCOPY can only be set ``False``.
| - WRITEBACKIFCOPY can only be set ``False``.
| - ALIGNED can only be set ``True`` if the data is truly aligned.
| - WRITEABLE can only be set ``True`` if the array owns its own memory
| or the ultimate owner of the memory exposes a writeable buffer
| interface or is a string.
|
| Arrays can be both C-style and Fortran-style contiguous simultaneously.
| This is clear for 1-dimensional arrays, but can also be true for higher
| dimensional arrays.
|
| Even for contiguous arrays a stride for a given dimension
| ``arr.strides[dim]`` may be *arbitrary* if ``arr.shape[dim] == 1``
| or the array has no elements.
| It does *not* generally hold that ``self.strides[-1] == self.itemsize``
| for C-style contiguous arrays or ``self.strides[0] == self.itemsize`` for
| Fortran-style contiguous arrays is true.
|
| flat
| A 1-D iterator over the array.
|
| This is a `numpy.flatiter` instance, which acts similarly to, but is not
| a subclass of, Python's built-in iterator object.
|
| See Also
| --------
| flatten : Return a copy of the array collapsed into one dimension.
|
| flatiter
|
| Examples
| --------
| >>> x = np.arange(1, 7).reshape(2, 3)
| >>> x
| array([[1, 2, 3],
| [4, 5, 6]])
| >>> x.flat[3]
| 4
| >>> x.T
| array([[1, 4],
| [2, 5],
| [3, 6]])
| >>> x.T.flat[3]
| 5
| >>> type(x.flat)
| <class 'numpy.flatiter'>
|
| An assignment example:
|
| >>> x.flat = 3; x
| array([[3, 3, 3],
| [3, 3, 3]])
| >>> x.flat[[1,4]] = 1; x
| array([[3, 1, 3],
| [3, 1, 3]])
|
| imag
| The imaginary part of the array.
|
| Examples
| --------
| >>> x = np.sqrt([1+0j, 0+1j])
| >>> x.imag
| array([ 0. , 0.70710678])
| >>> x.imag.dtype
| dtype('float64')
|
| itemsize
| Length of one array element in bytes.
|
| Examples
| --------
| >>> x = np.array([1,2,3], dtype=np.float64)
| >>> x.itemsize
| 8
| >>> x = np.array([1,2,3], dtype=np.complex128)
| >>> x.itemsize
| 16
|
| nbytes
| Total bytes consumed by the elements of the array.
|
| Notes
| -----
| Does not include memory consumed by non-element attributes of the
| array object.
|
| Examples
| --------
| >>> x = np.zeros((3,5,2), dtype=np.complex128)
| >>> x.nbytes
| 480
| >>> np.prod(x.shape) * x.itemsize
| 480
|
| ndim
| Number of array dimensions.
|
| Examples
| --------
| >>> x = np.array([1, 2, 3])
| >>> x.ndim
| 1
| >>> y = np.zeros((2, 3, 4))
| >>> y.ndim
| 3
|
| real
| The real part of the array.
|
| Examples
| --------
| >>> x = np.sqrt([1+0j, 0+1j])
| >>> x.real
| array([ 1. , 0.70710678])
| >>> x.real.dtype
| dtype('float64')
|
| See Also
| --------
| numpy.real : equivalent function
|
| shape
| Tuple of array dimensions.
|
| The shape property is usually used to get the current shape of an array,
| but may also be used to reshape the array in-place by assigning a tuple of
| array dimensions to it. As with `numpy.reshape`, one of the new shape
| dimensions can be -1, in which case its value is inferred from the size of
| the array and the remaining dimensions. Reshaping an array in-place will
| fail if a copy is required.
|
| Examples
| --------
| >>> x = np.array([1, 2, 3, 4])
| >>> x.shape
| (4,)
| >>> y = np.zeros((2, 3, 4))
| >>> y.shape
| (2, 3, 4)
| >>> y.shape = (3, 8)
| >>> y
| array([[ 0., 0., 0., 0., 0., 0., 0., 0.],
| [ 0., 0., 0., 0., 0., 0., 0., 0.],
| [ 0., 0., 0., 0., 0., 0., 0., 0.]])
| >>> y.shape = (3, 6)
| Traceback (most recent call last):
| File "<stdin>", line 1, in <module>
| ValueError: total size of new array must be unchanged
| >>> np.zeros((4,2))[::2].shape = (-1,)
| Traceback (most recent call last):
| File "<stdin>", line 1, in <module>
| AttributeError: incompatible shape for a non-contiguous array
|
| See Also
| --------
| numpy.reshape : similar function
| ndarray.reshape : similar method
|
| size
| Number of elements in the array.
|
| Equal to ``np.prod(a.shape)``, i.e., the product of the array's
| dimensions.
|
| Notes
| -----
| `a.size` returns a standard arbitrary precision Python integer. This
| may not be the case with other methods of obtaining the same value
| (like the suggested ``np.prod(a.shape)``, which returns an instance
| of ``np.int_``), and may be relevant if the value is used further in
| calculations that may overflow a fixed size integer type.
|
| Examples
| --------
| >>> x = np.zeros((3, 5, 2), dtype=np.complex128)
| >>> x.size
| 30
| >>> np.prod(x.shape)
| 30
|
| strides
| Tuple of bytes to step in each dimension when traversing an array.
|
| The byte offset of element ``(i[0], i[1], ..., i[n])`` in an array `a`
| is::
|
| offset = sum(np.array(i) * a.strides)
|
| A more detailed explanation of strides can be found in the
| "ndarray.rst" file in the NumPy reference guide.
|
| Notes
| -----
| Imagine an array of 32-bit integers (each 4 bytes)::
|
| x = np.array([[0, 1, 2, 3, 4],
| [5, 6, 7, 8, 9]], dtype=np.int32)
|
| This array is stored in memory as 40 bytes, one after the other
| (known as a contiguous block of memory). The strides of an array tell
| us how many bytes we have to skip in memory to move to the next position
| along a certain axis. For example, we have to skip 4 bytes (1 value) to
| move to the next column, but 20 bytes (5 values) to get to the same
| position in the next row. As such, the strides for the array `x` will be
| ``(20, 4)``.
|
| See Also
| --------
| numpy.lib.stride_tricks.as_strided
|
| Examples
| --------
| >>> y = np.reshape(np.arange(2*3*4), (2,3,4))
| >>> y
| array([[[ 0, 1, 2, 3],
| [ 4, 5, 6, 7],
| [ 8, 9, 10, 11]],
| [[12, 13, 14, 15],
| [16, 17, 18, 19],
| [20, 21, 22, 23]]])
| >>> y.strides
| (48, 16, 4)
| >>> y[1,1,1]
| 17
| >>> offset=sum(y.strides * np.array((1,1,1)))
| >>> offset/y.itemsize
| 17
|
| >>> x = np.reshape(np.arange(5*6*7*8), (5,6,7,8)).transpose(2,3,1,0)
| >>> x.strides
| (32, 4, 224, 1344)
| >>> i = np.array([3,5,2,2])
| >>> offset = sum(i * x.strides)
| >>> x[3,5,2,2]
| 813
| >>> offset / x.itemsize
| 813
|
| ----------------------------------------------------------------------
| Data and other attributes inherited from ndarray:
|
| __hash__ = None
A.5.3 Matrix computations
- The sub-module
numpy.linalgimplements basic linear algebra, such as solving linear systems, singular value decomposition, etc.
A.5.3.1 Inverse
A.5.4 Data processing and reshaping
Often it is useful to store datasets in Numpy arrays. Numpy provides a number of functions to calculate the statistics of datasets in arrays.
When functions such as min, max, etc. are applied to a multidimensional arrays, it is sometimes useful to apply the calculation to the entire array, and sometimes only on a row or column basis. Using the axis argument we can specify how these functions should behave:
array([[0.31751608, 0.41545447, 0.94062331],
[0.17379774, 0.57561705, 0.31818086],
[0.40848656, 0.62145644, 0.79010869]])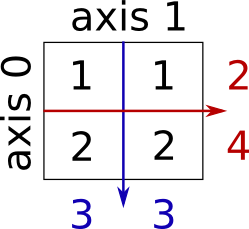
Many other functions and methods in the array and matrix classes accept the same (optional) axis keyword argument.
The shape of a Numpy array can be modified without copying the underlying data, which makes it a fast operation even for large arrays.
array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24],
[30, 31, 32, 33, 34],
[40, 41, 42, 43, 44]])array([[ 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30,
31, 32, 33, 34, 40, 41, 42, 43, 44]])With newaxis, we can insert new dimensions in an array, for example converting a vector to a column or row matrix:
A.5.4.1 Stacking and repeating arrays
Using function repeat, tile, vstack, hstack, and concatenate we can create larger vectors and matrices from smaller ones:
A.6 Copy and “deep copy”
- To achieve high performance, assignments in Python usually do not copy the underlying objects. This is important for example when objects are passed between functions, to avoid an excessive amount of memory copying when it is not necessary (technical term: pass by reference).
- A slicing operation creates a view on the original array, which is just a way of accessing array data. Thus the original array is not copied in memory.
If we want to avoid this behavior, so that when we get a new completely independent object B copied from A, then we need to do a so-called “deep copy” using the function copy:
[[-5 2]
[ 3 4]]
[[10 2]
[ 3 4]]A.6.1 Memory layout matters!
A.7 Iterating over array elements
Generally, we want to avoid iterating over the elements of arrays whenever we can (at all costs). The reason is that in an interpreted language like Python (or MATLAB), iterations are really slow compared to vectorized operations.
585 µs ± 24.1 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)15.2 µs ± 892 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)17.9 µs ± 454 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)2.86 µs ± 171 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)A.7.1 Create Your Own Vectorizing functions
To get good performance we should try to avoid looping over elements in our vectors and matrices, and instead use vectorized algorithms. The first step in converting a scalar algorithm to a vectorized algorithm is to make sure that the functions we write work with vector inputs.
To get a vectorized version of Theta we can use the Numpy function vectorize. In many cases it can automatically vectorize a function:
A.7.2 Type casting
Since Numpy arrays are statically typed, the type of an array does not change once created. But we can explicitly cast an array of some type to another using the astype functions (see also the similar asarray function). This always creates a new array of a new type:
array([[0.40570044, 0.66548144, 0.13835937, 0.83043309, 0.12319969],
[0.58779155, 0.06309849, 0.49710274, 0.92839462, 0.80603084],
[0.19839124, 0.34528354, 0.53473647, 0.97858347, 0.5030445 ],
[0.3474475 , 0.21278653, 0.17745402, 0.1040286 , 0.18745545],
[0.04031375, 0.23991727, 0.5462427 , 0.20778317, 0.99270398]])array([[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True]])- See casting at https://scipy-lectures.org/intro/numpy/elaborate_arrays.html
A.8 File I/O
- NumPy has its own binary format, not portable but with efficient I/O
- Useful when storing and reading back numpy array data. Use the functions
numpy.saveandnumpy.load - Matlab: scipy.io.loadmat, scipy.io.savemat
array([[0.40570044, 0.66548144, 0.13835937, 0.83043309, 0.12319969],
[0.58779155, 0.06309849, 0.49710274, 0.92839462, 0.80603084],
[0.19839124, 0.34528354, 0.53473647, 0.97858347, 0.5030445 ],
[0.3474475 , 0.21278653, 0.17745402, 0.1040286 , 0.18745545],
[0.04031375, 0.23991727, 0.5462427 , 0.20778317, 0.99270398]])A.9 Conclusion
To make the code faster using NumPy and - Vectorizing for loops: Find tricks to avoid for loops using numpy arrays.
In place operations:
a *= 3instead ofa = 3*aUse views instead of copies whenever possible
Memory arrangement is important. Keep strides small as possible for coalescing memory access
Broadcasting: Use broadcasting to do operations on arrays as small as possible before combining them.
Use compiled code (The following session)
A.10 References
- https://scipy-lectures.org/intro/numpy/index.html - A good introduction to pydata stack
- https://github.com/jrjohansson/scientific-python-lectures/blob/master/Lecture-2-Numpy.ipynb - A good introduction for NumPy though a bit of outdated
- http://cs229.stanford.edu/section/cs229_python_tutorial/Spring_2020_Notebook.html - Another good introduction to NumPy
- https://www.pythonlikeyoumeanit.com/Module3_IntroducingNumpy/Broadcasting.html - A great reference for broadcasting and distance calculation
- https://eli.thegreenplace.net/2015/memory-layout-of-multi-dimensional-arrays- A great article for memory layout behind NumPy
- https://numpy.org/doc/stable/user/numpy-for-matlab-users.html - A Numpy guide for MATLAB users
- http://mathesaurus.sourceforge.net/r-numpy.html - A Numpy guide for R users